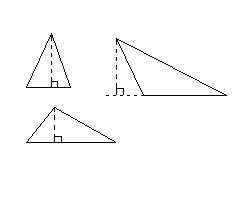![]() You don't need to be an 'investor' to invest in Singletrack: 6 days left: 95% of target - Find out more
You don't need to be an 'investor' to invest in Singletrack: 6 days left: 95% of target - Find out more
And before any genius comes lumbering with 1/2 x b x h...
If you have a 3 sides of known length but unknown angles, whats the formula for area?
Ah back to school days of trigonometry...
http://www.mathgoodies.com/lessons/vol1/area_triangle.html
D-
back of the class.
Thats just loads of different ways of using 1/2 b h
Simple. Just use Wolfram Alpha:
Triangle with sides 10, 20, 20:
http://www.wolframalpha.com/input/?i=area+of+triangle+10+20+20
crazy legs & Olly, both fail
See me after class....
Graham, A+.
Top of the class, and you get to wear your house tie on Founder's day.
HipHip
If you have a 3 sides of known length but unknown angles
I'm fairly certain that that isn't possible. Simple use of the cosine law (essentially a variant of pythagoras) will allow you to determine the angles. Just because they aren't explicitly state does not mean that they are "unknown".
What, it still gives you the area of the triangle!
To find the angles you need
sin theta = opp/hyp
cos theta = opp/hyp
tan theta = opp/adj
I'm fairly certain that that isn't possible
of course it's possible 🙂 Yes the angles are fixed by the lengths of the sides but you may not know the answer or have a protractor. There is a difference between unknown and unknowable, and between [b]someone [/b]knowing and you knowing
No, what I meant was that you can't have a triangle where you know the lengths of the sides and not the angles. The stuff you've listed is only valid for a right angled triangle. What I meant was
a^2=b^2+c^2 - 2bccosA
Since you know all the lengths (a,b,c) the calculation of the angle A is trivial.
Also I wouldn't be surprised if the method GrahamA is only another representation of 1/2bh. I just can be bothered to do the algabraic manipulation right now.
indeed I was looking for a more "Euclidean" geometry technique using the known sides, rather than have to go into trigonometry.
There is a difference between unknown and unknowable, and between someone knowing and you knowing
Not in Maths there isn't.
No, what I meant was that you can't have a triangle where you know the lengths of the sides and not the angles
I understand what you mean, but you are not saying it correctly. I can easily invent a triangle, say one with sides 3, 4 and 6 cm. I know the sides and so do you. Neither of us know the angles though we could find out, so they are currently unknown.
One could invent a triangle with sides 3, 4 and 100000 cm for which the angles are truly unknown and unknowable in this universe 🙂
One could invent a triangle with sides 3, 4 and 100000 cm for which the angles are truly unknown and unknowable in this universe
[url= http://www.wolframalpha.com/input/?i=area+of+triangle+3cm+4cm+100000cm ]0 + 250,000 [i]i[/i] m²[/url] 🙂
Neither of us know the angles though we could find out, so they are currently unknown.
Simon the angles are defined by the lengths and are therefore not an "unknown" in the mathamatical sense of the word, they just aren't explicitly stated.
One could invent a triangle with sides 3, 4 and 100000 cm for which the angles are truly unknown and unknowable in this universe
No, the method for calculating the angles of such a triangle is exactly the same as I previously described. Don't confuse "can't be done" with "I can't do it"
crazy legs & Olly, both fail
See me after class....
there is only one situtation i can think of where 1/2 * B * H doesnt work, and thats when its not a triangle.
how on earth does it not work?
Don't confuse "can't be done" with "I can't do it"
Well no, he's right in that such a triangle can't exist in our 2D space so any measurement of area and angles is basically impossible and can only be supposed upon by using imaginary numbers and other such mathematical smoke.
because with three known sides and no EXPLICITLY stated angles you cant determine "h" readily.
Graham's formula was what I was after.
Its a method for effectively indirectly deriving h and solving Area from the lengths at hand.
The formula is need for dim propertymonkeys who have difficulty turning the calculator on, let alone SOHCAHTOA
Olly - in your diagram if I gave you the lengths of the sides in bold, can you derive the dotted line without using trig?
Well no, he's right in that such a triangle can't exist in our 2D space so any measurement of area and angles is basically impossible and can only be supposed upon by using imaginary numbers and other such mathematical smoke.
so his mistake is
One could invent a triangle with sides 3, 4 and 100000 cm
Which you can't. That'll teach me to read stuff properly.
Graham's formula was what I was after.
It's Heron's Formula by the way not mine 😀 :
http://mathworld.wolfram.com/HeronsFormula.html
I'm a mathematical klutz which is why I keep the Wolfram sites handy 😳
If you know the lengths of all three sides then you know (can calculate) the angles - assuming the triangle is on a flat surface (of course you can also work them out for other surfaces like spheres or cylinders too).
There's a nice explanation of hero's or heron's formula here.
http://www.karlscalculus.org/hero.html
porterclough - you're using trig again 🙄
cheers Dave. Longtime no hear. You guys all well?!
Olly - in your diagram if I gave you the lengths of the sides in bold, can you derive the dotted line without using trig?
Yes
pretty basic trig surely?
so is the question more "how can [b]I[/b] work it out"? ;p
I give up.
you give up as in you give up trying to work out how to do it, or you give up trying to explain to us monkeys that it ISNT as simple a question as youve actually written?
what are the 3 side lengths?
x
SOHCAHTOA only works for right angled triangles anyway doesn't it?
specifically without using trig
I know I should have made that clearer in the OP, but I assumed most people knew you could do it with trig if so minded.
I wanted a simple method using non-trig algebra and assumed there was some kind of Euclidean solution.
SOHCAHTOA works for any type of triangle. Although, does it work for imaginary ones? 🙂
One could invent a triangle with sides 3, 4 and 100000 cm for which the angles are truly unknown and unknowable in this universe
and more importantly, not a triangle??
are we thinking in 4th and 5th dimensions or something?
Olly:pretty basic trig surely?
..
what are the 3 side lengths?
For argument sake let's say 23, 25, and 27cm.
Go for it and show your working. If you come up with something simpler than Heron's I'll be impressed 🙂
I know I should have made that clearer in the OP, but I assumed most people knew you could do it with trig if so minded.
lol, to me that reads "i assume most people already know how to use trig, so would automatically by pass it and go to a different method"
anyhoo, i still refer you to the FIRST link on google :p
Hi Mark, yeah we're all good thanks, fancy a ride tomorrow afternoon?
we worked it out as 277.6 (rightly or wrongly)
i still resent being told im "wrong" just because you didnt word the question properly.
there was a teacher once at school, who asked a simple, question in a test, got a simple answer, and then failed us (the whole class) cause we hadnt used the method he wanted, but he didnt SPECIFY what he wanted.
we worked it out as 277.6
Show your working boy! No mark. See me after class.
i still resent being told im "wrong"
I've got bad news for you there... 😉
Dave - sorry, stuck in London tomorrow.
another time though.
SOHCAHTOA works for any type of triangle
And there I was thinking that only right angle triangles had Hippopotamuses
The hours just fly by for you guys, huh?
So how do you work it out?
[i]So how do you work it out?[/i]
I think the gist of it is that any triangle can be thought of as 2 triangles containing right angles (imagine drawing a dotted line through it). For both these triangles you know the length of the side opposite the right angle so you can use trig (SOCAHTOA) to find the lengths of the other 2 sides. Then for each triangle you do b*h*0.5 and add the results.
EDIT: Er, or maybe not!
EDIT AGAIN: No, that's right 🙂
I think the gist of it is that any triangle can be thought of as 2 triangles containing right angles (imagine drawing a dotted line through it).
That is how I would've done it.... But after reading this thread, I'm well confussed!!
MrSalmon: I think if you're going for that method then you have to use the [url= http://en.wikipedia.org/wiki/Law_of_cosines ]Law of Cosines[/url] first to get the angles.
Do you need the angles? If you have split your triangle into two right angled triangles by dropping a perpendicular line from C in GrahamS diag to the side AB. Then you don't know the length of this line, say h. Likewise you dont know how far along it intersects along side AB, assume the distance is x from A. Using Pythagoras, you know b^2 = x^2 + h^2 and you also know a^2= (c-x)^2 + h^2, solve for h and x and work out the areas and add together.
On you go then...
mefty - for help, read the link in inigo's post.
The algebraic manipulation is stepped through very nicely in there.
If my algebra is right, and it has been a while since I've had to do stuff like this, then that should work as it should simplify to
2x^2+2cx+a^2-b^2-c^2 = 0.
You will need to solve the resultant quadratic equation which granted isn't as easy as that other formula but still doesn't require the use of any trig.