You don't need to be an 'investor' to invest in Singletrack: 6 days left: 95% of target - Find out more
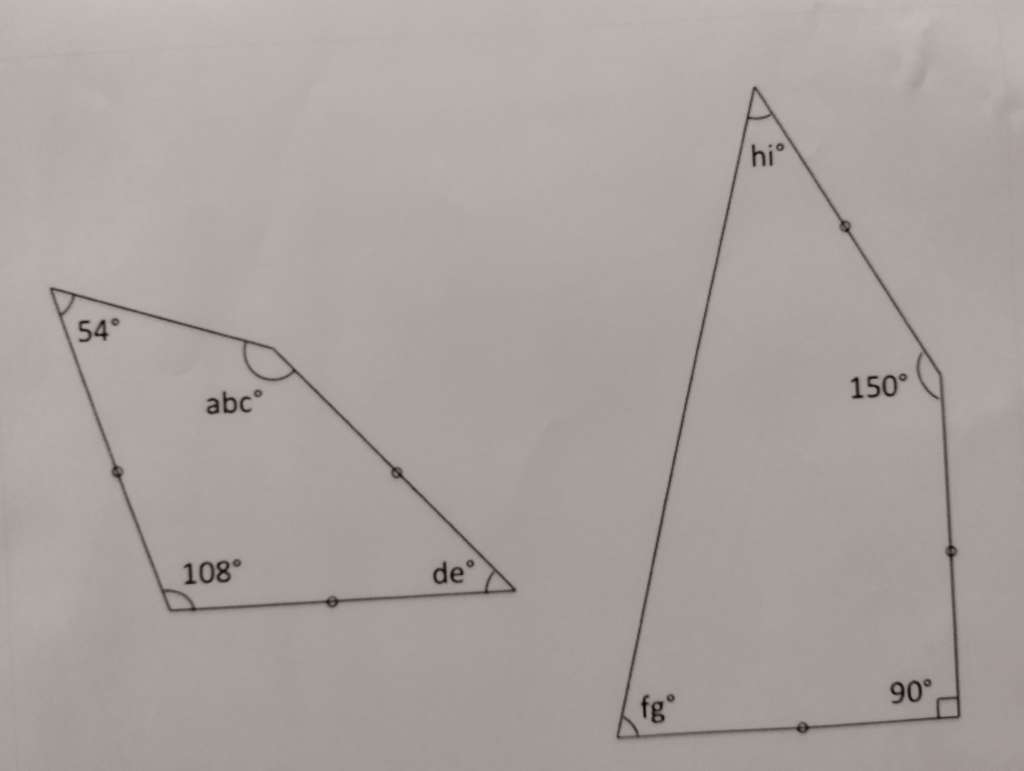
My daughter found this and expects me to solve it. The reputation for omniscience that I used to have has been coming under question lately so it's essential that I solve it or she will lose all respect for me.
.
42
42
Excellent, thank you. So looking forward the looks of awe I will receive when I announce the solution.
My hunch is that you’ll need non right angle trig and then set up simultaneous equations.Blimey, primary schools are setting some pretty tricky homework tasks nowadays.
My hunch is that you’ll need non right angle trig and then set up simultaneous equations.
Yeah, I started down a similar path then realized that I'd forgotten all the stuff I knew when I was 18 and couldn't be bothered trying to figure it all out again.
I would say you are going to need a combination of internal and external angles.
Try this for starters:
https://www.bbc.co.uk/bitesize/guides/zshb97h/revision/6#
No I haven't worked it out for you.
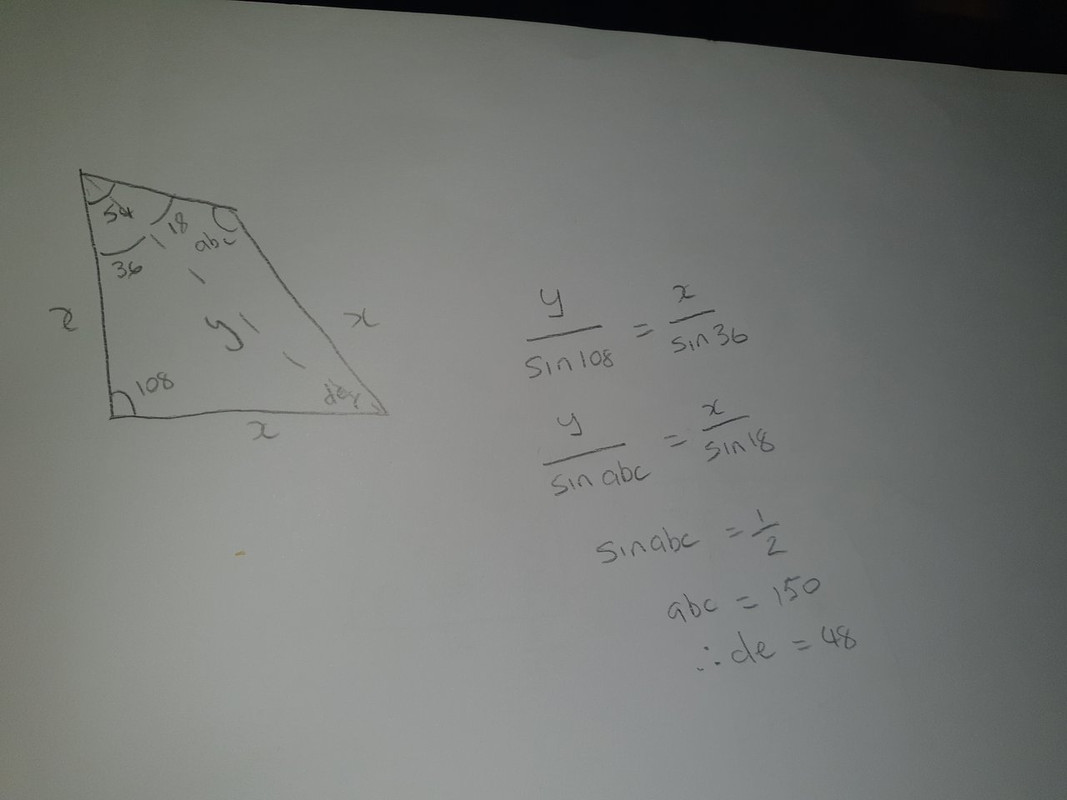
abc = 150
de = 48
Not seeing fg or hi.
fg = 75
hi = 45
Thanks, much appreciated.
That's waaaaay over the top.
The angles of a triangle always equal 180degrees.
You can draw a line through both those shapes to isolate one of the unknowns hi and ABC in those examples.
That gives you enough to find the other two.
Give me a sec and I will draw it out.
Ignore that. Put my glasses on!
I am still pretty sure you can do it without trig though.
You know all the angles equal 360
You know the four triangles you can create all sum to 180
Which means you can get a formula for any unknown angle.
And you can simultaneous equation and substitution to solve.
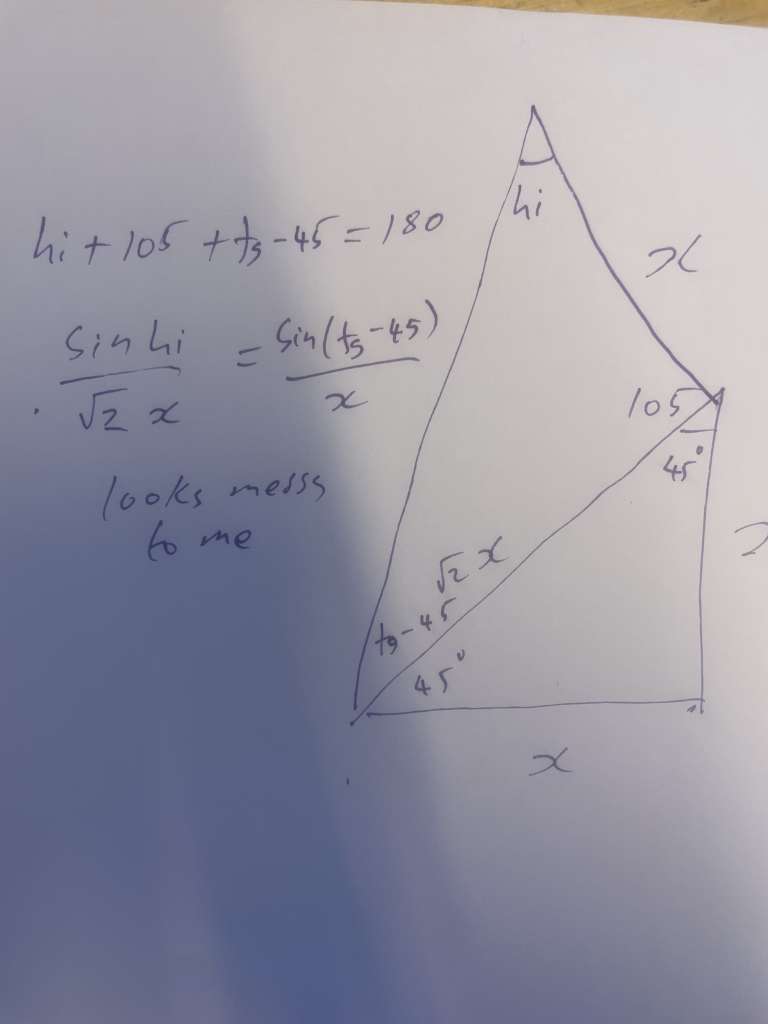
For the right hand figure:
Let the corners be A to D starting from the bottom left anticlockwise
Sides AB=BC=CD.=1, AC=1.414 (root 2)
Then for triangle ACD, using the Cosine Rule,
AD=1.414, CD=1, included angle=105, angle di=45
Angle fg = 360-(105+90+45) = 75
Haven't tried it for the other figure yet.
Correction::<br />In line 4, should read AC=1.414
By drawing a line from the top of the right hand figure to the bottom right, you can form two equilateral triangles. You can then solve the angles using nothing more complicated than subtracting and dividing by two.
Which leads me to expect that a similar simple solution exists for the left hand figure...
Ignore my last post, I don't think I am confident that my reasoning is sound, I've looked again and I'm not convinced the larger triangle when the right hand figure is divided as I describe is equilateral by anything more than coincidence... Bother.
ETA: Yes it is, but some basic trig *is* needed after all, it's not just simple sums after all.
For the left-hnd figure:
Let the corners be A to D starting at the bottom left anticlockwise,<br />Using the Cosine Rule - BD=1.618, then for triangle ABD angle at B=angle at D=36.<br />So for triangle BCD - BD=1.618, BC=1, angle at D=54-36=18<br />Using Cosine Rule - angle abc=132<br />Then angle de= 360-(108+54+132) = 66
Right hand one you can do with no trig...
You can complete the square using the two similar sides and the right angle. That then gives a 60 degree angle (150 - 90) between the top of the square and the third similar side. That is therefore an equilateral triangle, so you can complete the last side of that.
That then forms an isosceles triangle with the long diagonal... with a known angle of 150, therefore the other two angles are 15... which means hi is 60 - 15... so 45.
Like this, fg is 90 - 15.. so 75
Will think about the left hand one...
clue simple trigonometry is all that’s needed.<br /><br />
Ha! You say that, but…
What do the dots on the lines represent?
The dots mean those sides are the same length...