[Closed] Another Algebra question?

7+x = y*14

x=y*14-7

14y=7+x

x=14y-7 ?

still so far from being a BH 😥

y=(7+x)/14

Multiply both sides by 14 to get

14y = 7 + x

Shift the 7 over to the left

14y - 7 = x

x=14y-7, i got that but i had a brain fart and came up with some other random answers. Think my brain is overloaded cos that's an easy one.

Thanks for setting my mind at rest. May have more soon 🙂

FYI

http://www.wolframalpha.com/input/?i=y%3D%287%2Bx%29%2F14+solve+for+x

And you can even click "show steps".

ok just when u think you are getting somewhere a problem occurs.

Quadratic equations and factoring 🙂 up until now i have found it easy to factor them out but following all the rules in my coursework does not explain how 2x^2 affects the formula before factoring

So--- 2x^2+18x+14=0 becomes (2x ) (x )is as far as i get.

For the life of me i cant figure this one out. So how does 2x^2 affect the 18x and 14. Thanks

Basically you're going to have to take the square root of the right hand side when solving for x.

Edit: which means you get two possible results as a square root can be negative or positive.

I thought quadratic equations had no roots?

Does this help?

[url= http://www.wolframalpha.com/input/?i=2x^2%2B18x%2B14%3D0+solve+for+x ]Wolfram[/url]

Divide the whole lot by 2, which gives x^2+9x+7, so then you need two numbers that add to give -9 and multiply to give +7. Can't do that in my head 🙂

Follow the Wolfram link. Press "Show Steps"

Nick that is what i thought. Just needed clarification cos i cannot figure it out 🙂

The wolfram link is solving by 'completing the square' because the equation given doesn't factorise easily. Better to use the quadratic formula in this case. What course ate you studying?

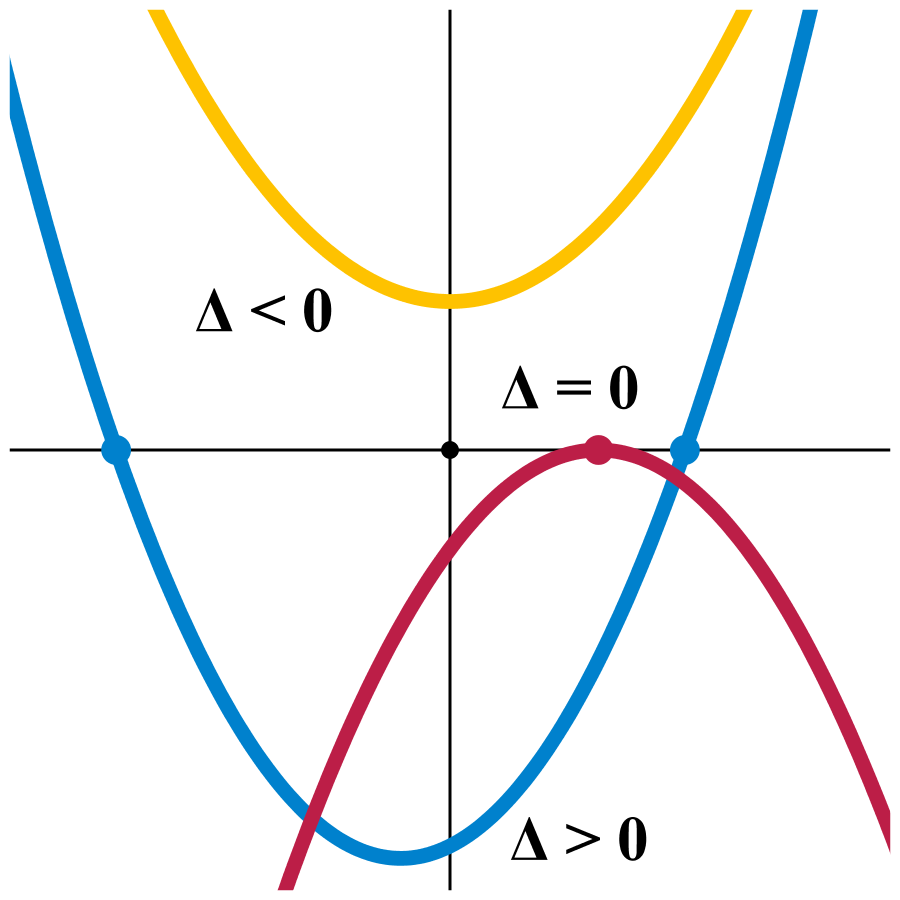
Ok quadratics always have either two roots, or no roots.

[img] [/img]

So ignoring the funky triangles, we can see the blue quadratic has two roots. The yellow quadratic doesn't have any. The red quadratic looks like it only has one, but this is what we call a repeated root, and thus it's defined to still have two.

For example, y=(x-1)^2 or y=(x-1)(x-1) ----- these are both the same, and have a repeated root at x=1.

2x^2+18x+14=0

First of all we can divide everything by 2. This doesn't really help much except to make it look nicer.

x^2 + 9x + 7 = 0

Well to convert that to the form (x+m)(x+n) ----- as we know we can do with quadratics (also remember m and n can be negative) ------- we need m*n = 7 and m + n = 9.

Well 7 is prime so the only two integers are 7 and 1, but they don't add together to equal 9. So we need to use the formula.

[img] [/img]

Do you know how to use this?

No man, way above me at the moment. I have factored a lot of quadratic equations so far but they were all x^2 at the beginning etc etc not 2x^2

Are you sure you've got the question right then as that equation is a hard one. What course? What level?

2x^2+18x+14=0

There's a formula for this.

Where ax^2+bx+c=0

.

    -b +/- sqrt(b^2 -4ac)
x = ---------------------
            2a

So your equation has a=2, b=18, c=14.

.

    -18 +/- sqrt(18^2 - (4*2*14))
x = -----------------------------
            2*2

    -18 +/- sqrt(324 - 112)
x = -----------------------
             4

    -18 +/- 14.56
x = -------------
         4

x = -0.86  or  -8.14

I think, anyway. Been a while.

There's a formula for this.

Where ax^2+bx+c=0

Aye, called the quadratic equation I believe!

Who'd a thunk it.

Mac, the question requires use of the formula, so if you haven't been taught how to use it yet, you may have read the question wrongly.

If not, quadratics are of the form a*x^2 + b*x + c = 0

So find a, b, and c, plug them into the formula, and you should get two answers. If you use these answers as x in the original question, you should get 0 as the answer, confirming your result.

the question requires use of the formula, so if you haven't been taught how to use it yet, you may have read the question wrongly.

Good point, well made.

Oops double post.

Realman,thanks for that. It explains a lot.

Happy to help. Maths can be fun, just a lot of people have a big phobia about it. You've got my respect for giving it a go. Good luck in your coursework/exams.

Cheers bud 🙂 aye its ace when u finally figure out a problem that you cant get for days.